Differential Privacy
This article explains Differential Privacy at a high level, without getting too technical and describing its importance in real world applications.
Differential privacy: General concept
Differential Privacy is a formal mathematical framework for quantifying and managing privacy risks.
Cynthia Dwork, co-creator of the concept, defines it in simple language as follows: "The outcome of any analysis is essentially equally likely; independent of whether any individual joins, or refrains from joining the dataset" Cynthia Dwork, 2016.
Differential Privacy provides demonstrable privacy and protection against a wide range of possible attacks, including those that are currently unforeseen. Fundamentally, what is sought with differential privacy is that: "Adding or removing the data record of a single individual does not change the probability of any result too much" Kearns & Roth, 2020.
Approach to Differential Privacy: Randomized Response and Plausible Deniability
Especially in studies in the social sciences, there is a way to obtain answers or usefulness in surveys, but at the same time maintain the privacy or “plausible deniability” of the participants, this is particularly useful when the questions are controversial. The basic concept of the procedure is as follows:
- The participant is asked a controversial question, and to toss a coin
- If heads, then the participant must answer the question honestly.
- If tails come up, then the participant must flip another coin, answering “yes” if heads, and “no” if tails. Independent of whether the true answer was yes or no
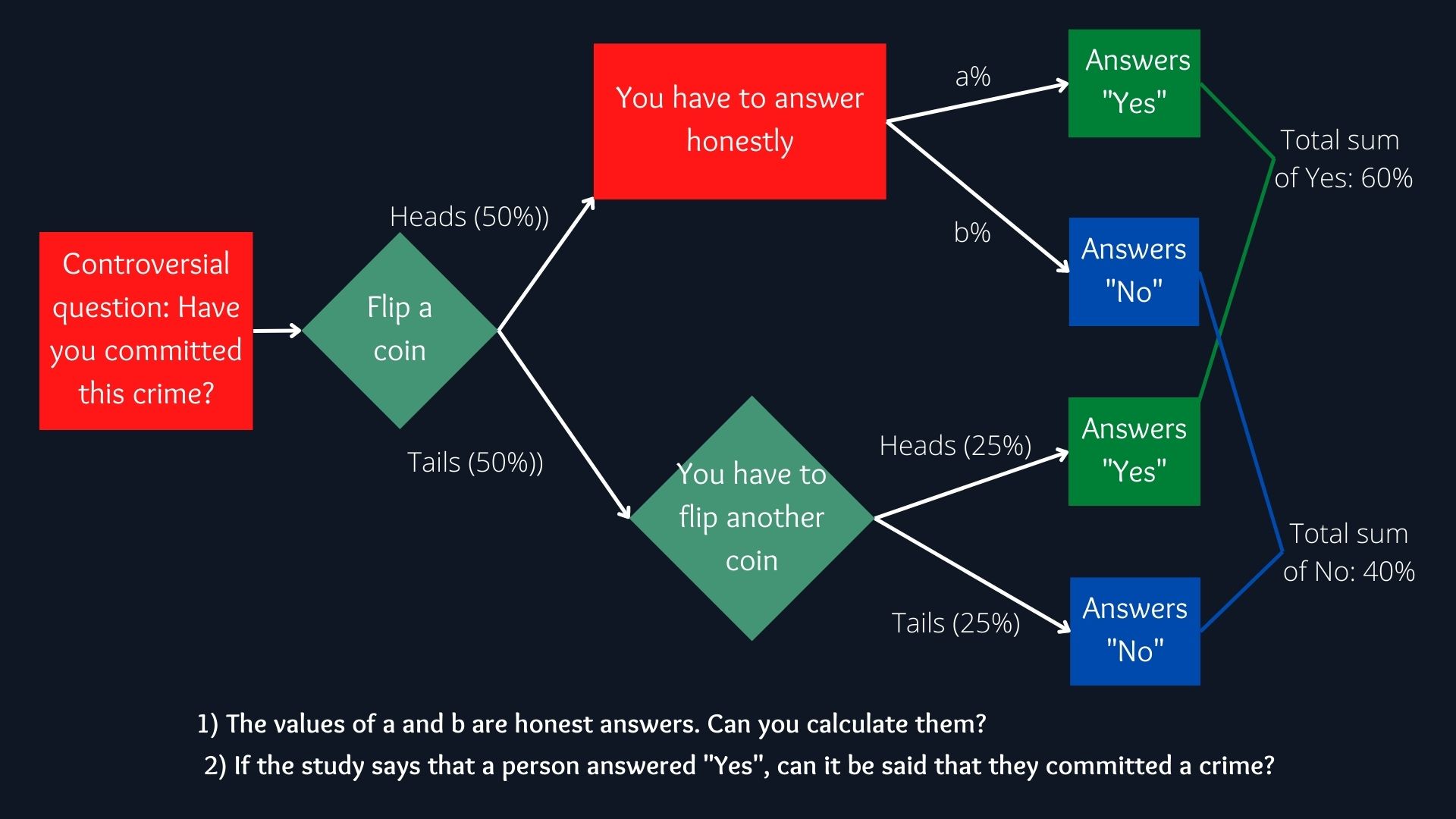
Usefulness of the data: Can you find out how many respondents actually answered “yes” and how many answered “no”? From the figure it can be obtained (in a more or less intuitive way) that the result is: True Yes: 70% True No: 30%
Formally:
TY = HY + FYWhere:
HY = Honest Yes;
FY = False Yes
Clearing:
TY = HY + FY = 0.6 - 0.25 = 0.35 The probability of finding a true “Yes” is 0.35, however, this is within the total number of respondents, that is, both those who answered honestly and those who did not. If only the set of those who answered honestly is taken, with probability p -probability of getting heads when tossing a coin-, then those who answered yes denoted by S:
Y = TY/p = 0.35/0.5 = 0.7 We have learned information about the general population, but not from any specific individual, as they have perfect deniability because we don't know if they answer truthfully or not. This concet is what Differential Privacy inherits.
Mathematical Definition of Differential Privacy
A random function K grants differential privacy if for all data sets D1 and D2 that differ by at most one element, and all S ⊆ Range(K) holds:
Pr[K(D1) ∈ S] ≤ exp(Ɛ) × Pr[K(D2) ∈ S], Where:
D1 and D2: Neighboring data sets that differ by at most one element
K: Randomized function, it is an operation that could be done on the database, for example "return the partial sum of the first i elements"
Why do we need Differential Privacy?
There are a number of notable incidents where Differential Privacy would have been useful. However, at the times it did not yet exist or was simply not applied:
In 2006, AOL delivered 20 million search queries corresponding to 650,000 users. As a privacy protection measure, they replaced user identifiers with random numbers, however, several users were re-identified due to the set of their searches. AOL removed the download link shortly after.
In 2006 Netflix held a public contest in order to improve its recommendation system, for which it released data from 500,000 users, trying to protect their identity by eliminating their identifiers. The data was crossed with the database of The Internet Movie Database (IMBd), with which it was possible to re-identify users who used both services.
Differential Privacy helps complying with privacy laws
Differential Privacy can help companies comply with data privacy regulations, such as the General Data Regulation Regulation (GDPR) in Europe and the California Consumer Privacy Act (CCPA), without undermining its ability to analyze the behavior of clients, that is, it protects the privacy of clients while obtaining useful information from the population studied. Failure to comply with privacy regulations can result in heavy penalties. According to the 2021 report of the law firm DLA Piper, from May 2018 to January 2021, fines worth 273 million euros have been imposed under the GDPR (DLA Piper GDPR Fines and Data Breach Survey, 2021) .Differential Privacy and Machine Learning
Machine learning algorithms work by studying large amounts of data and updating model parameters to encode relationships in that data. Ideally, we would prefer that the parameters of these machine learning models encode general patterns. For example: "Obese patients with poor sleep habits are more likely to develop diabetes"; rather than private data used in training, such as: "Peter has hypertension".
Unfortunately, machine learning algorithms do not learn to ignore these details by default. If we want to use machine learning to solve an important task, such as creating a diabetes detection model, then when we launch this machine learning model, we may also reveal training information without realizing it.
How does Machine Learning with Differential Privacy works
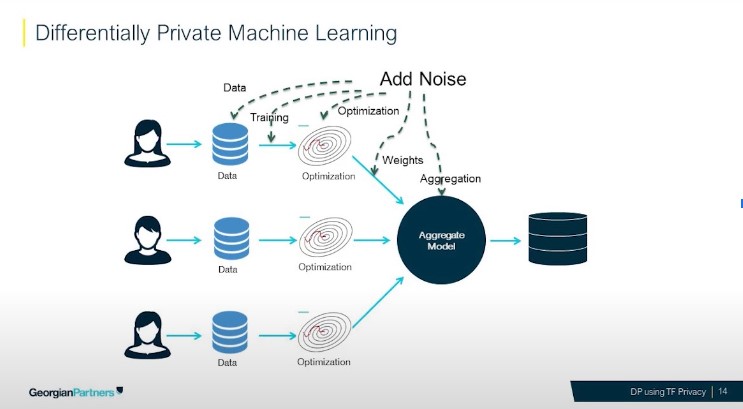
Source: Georgian Partners
Noise can be applied to achieve Differential Privacy in different training steps: in the data, in the training, the optimization, the weights and even in the aggregation process.Why do we need Differential Privacy while training Machine Learning models?
There are a number of real world uses for differential privacy in machine learning. Solving for legal, economic and ethical issues.
The Cold Start Problem:
In recommendation systems the cold start problem occurs when inferences cannot be draw due to not having enough gathered information.For example, you have a big client who wants to predict user retention, but as you are recently working for them, you don't have enough data to train a model yet.
Solution?
Using the data that can be applied from a similar client.
What's the problem with this solution?
The client from whom you are using the information probably does not want its sensitive data to be known, which can be extrated from the training of their models.
Enters Differential Privacy for Machine Learning models, protecting sensible data while giving utility from a larger pool of information (including that of all clients), making it so not only clients agree to share data, but they also wanna do it since it benefits them.